문제

3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

입력

첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.

출력

첫째 줄에 경우의 수를 출력한다.

예제 입력 1

1
2

예제 출력 1

1
3

내 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const N = +require("fs").readFileSync("/dev/stdin").toString().trim();

function fillTile(n) {
  const DP = [0, 0, 3];

  for (let i = 3; i <= n; i++) {
    if (i % 2 !== 0) {
      DP[i] = 0;
      continue;
    }
    let k = i - 2;
    DP[i] = DP[i - 2] * DP[2] + 2;
    while (k >= 2) {
      DP[i] += DP[k - 2] * 2;
      k -= 2;
    }
  }
  return DP[n];
}

console.log(fillTile(N));

해설

우선 n이 홀수인 경우는 경우의 수가 0이다.

그다음에 n이 4인 경우는 직접 그려보았다.

그랬더니 기존 유형을 벗어나는 특이한 모양 2개가 추가되는 것을 알 수 있었다.

DP[4] = DP[2] * 2 + 2 를 알 수 있었다.

n=4

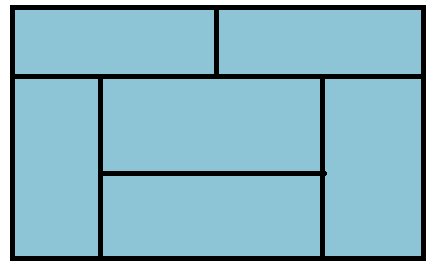
이러한 모양은 n이 6인 경우에도 나타났다.

n=6

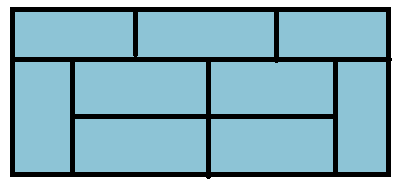
이를 토대로 점화식을 세워보았다.

DP[i] = DP[i-2] * DP[2] + DP[i-4] * 2 + DP[i-6] * 2 + … DP[2] * 2 + 2

  1. DP[i-2]에다가 DP[2]의 반복되는 패턴의 경우의 수를 곱해준다.
  2. 이후에는 특이한 케이스 2개씩 늘어나는 것만 고려해준다. 예를 들어 DP[2] * 2는 DP[i-2]에서의 특이 케이스 경우의 수를 의미한다.