문제

2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.

아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

https://onlinejudgeimages.s3-ap-northeast-1.amazonaws.com/problem/11726/1.png

입력

첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)

출력

첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.

예제

예제 입력 1

1
2
2

예제 출력 1

1
2
2

예제 입력 2

1
2
9

예제 출력 2

1
55

내 코드

1
2
3
4
5
6
7
8
9
10
11
const input = +require("fs").readFileSync("/dev/stdin").toString().trim();

const DP = [];
DP[1] = 1;
DP[2] = 2;

for (let i = 3; i <= input; i++) {
  DP[i] = (DP[i - 1] + DP[i - 2]) % 10007;
}

console.log(DP[input]);

패턴을 찾아보려고 노력했지만 결국 못찾고 다른 사람 코드를 보았다.. DP는 작은 문제에서 나온 결과물을 가지고 큰 문제를 해결하는 문제이다. 즉, 작은 문제의 결과물을 큰 문제에 결과물에 대입할 수 있는 안목이 필요하다.

위 문제는 2x1 타일을 가장 왼쪽에 세로로 배치했을 때, 2x1 타일을 가장 왼쪽에 가로로 2줄 배치했을 때 경우의 수로 나뉜다.

n = 1인 경우는 1가지이고, n = 2인 경우 2가지를 그림으로 그려본다.

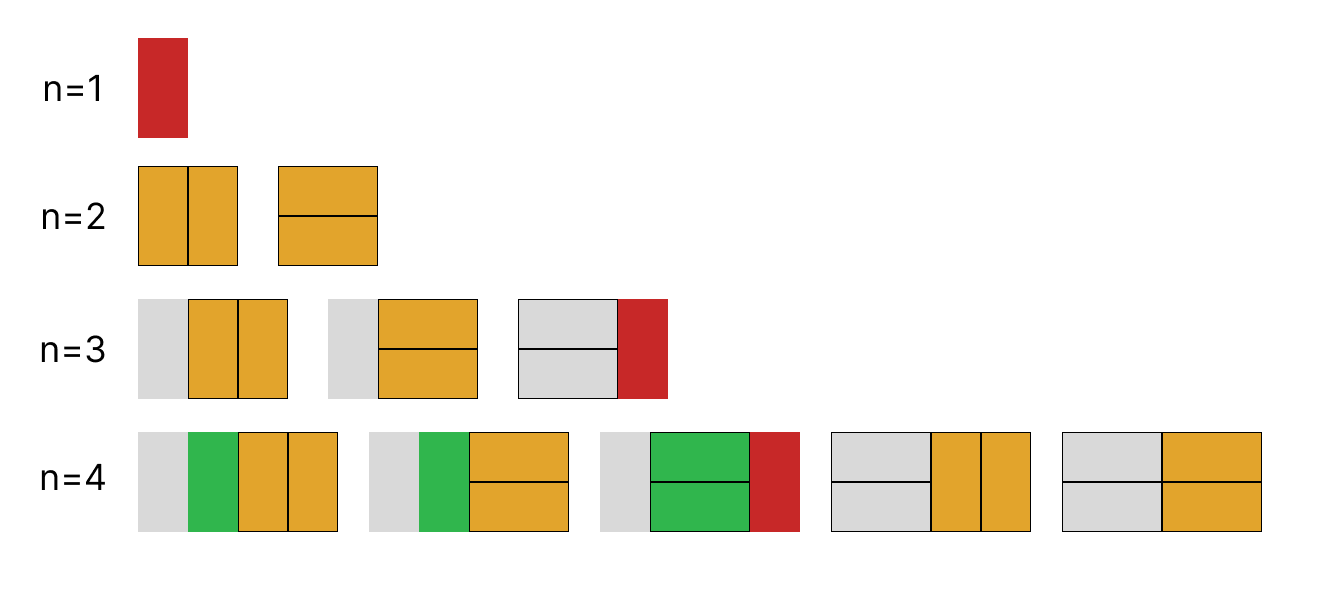
Frame 1.png

  • 즉, 왼쪽에 세로로 2x1을 배치했을 때 경우의 수는 n-1 경우의 수와 같고, 왼쪽에 가로로 2줄 배치했을 때경우의 수는 n-2의 경우의 수와 같다.
  • 따라서 DP[n] = DP[n-1] + DP[n-2]가 성립한다.