순열 알고리즘

코딩문제를 풀 때 중간 과정에서 자주 등장하는(?) 알고리즘으로 조합, 순열 알고리즘이 있다.

오늘은 백트랙킹과 DFS를 이용하여 순열 알고리즘을 구현하는 방법을 알아보자

순열

순열은 순서에 상관있게 n개의 원소 중에 r개를 중복없이 골라 나열하는 경우의 수

ex) [“a”,”b”,”c”] 배열에서 3개의 알파벳으로 단어를 만드는 경우의 수

순열과 조합 알고리즘을 이해하기 위해 백트래킹(tree 구조) 패턴으로 보면 이해가 쉽다.

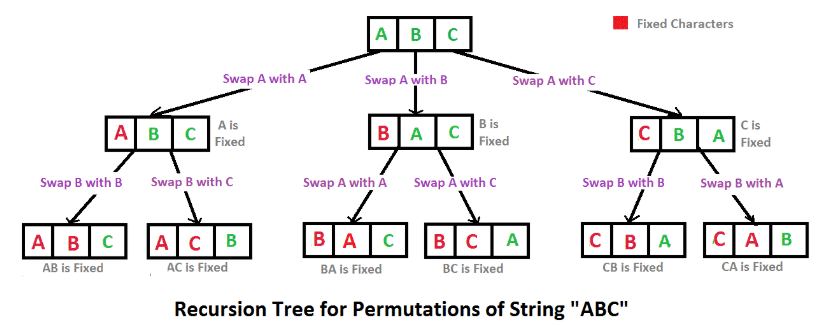
permutation

백트랙킹과 DFS(깊이 우선 탐색)으로 순열 알고리즘을 구현해보자

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function permutation(arr) {
  const result = [];

  // DFS
  const dfs = (i, arr) => {
    // base condition
    if (i === arr.length) {
      return result.push([...arr]);
    }
    for (let j = i; j < arr.length; j++) {
      // swap
      [arr[i], arr[j]] = [arr[j], arr[i]];
      // dfs
      dfs(i + 1, arr);
      // swap back
      [arr[i], arr[j]] = [arr[j], arr[i]];
    }
  };
  dfs(0, arr);
  return result;
}

  1. 배열의 각 위치를 나타내는 i, j가 있다고 생각하자. (i,j는 처음에 a 위치에서 시작한다)

  2. i가 배열의 길이만큼 커지면 그 때의 arr 배열값을 result 배열에 더해준다.

  3. i,j의 위치를 바꿔준다. dfs 함수를 재귀적으로 i+1로 호출한다.

그 결과 첫번째 result 배열에 담기는 값은 abc 이다.

이후 다시 원상복귀로 돌아오면서 i = 1일 때, 반복문이 j=2 < arr.length 조건에 만족하므로 a b c 요소에서 i = 1인 b 요소와 j = 2인 c 요소를 바꿔준다. (a c b)

이 후 dfs(i+1,arr) 함수 재귀로 호출하면 i = 2 = j가 되므로 a c b 위치가 바뀌지 않고 결국 i = arr.length가 되어 2번째로 출력되는 값은 acb 가 된다.

acb를 다시 원상 복귀 시킨 후 i = 1, j = 3으로 반복문이 종료되고 다시 처음이였던 i = 0 = j로 돌아오게 된다.

  1. 이제 반복문으로 i = 0, j++ 되어 j = 1이 되어 bac로 위치 바꿔주고 앞선 과정을 반복한다.

만약 재귀가 이해가 잘 안된다면 디버깅을 통해서 노트에 적어가면서 이해해보자. 사실 나도 2번째 보고 있는데 이해가 잘 안되서 자주 확인하기 위해 TIL을 작성하였다.